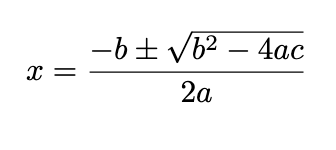
Wat is de ABC-formule?
Wanneer je een kwadratische vergelijking wilt oplossen, heb je een methode nodig om de waarden van x te vinden. Kwadratische vergelijkingen komen vaak voor in wiskunde, bijvoorbeeld bij het berekenen van oppervlakten, het vinden van snijpunten in grafieken of bij natuurkundige toepassingen. Een handige manier om deze vergelijkingen op te lossen is met de ABC-formule.
Zo gebruik je de ABC-formule
De ABC-formule gebruik je om kwadratische vergelijkingen (ax² + bx + c = 0) op te lossen.
Let op! Er moet een kwadraat in staan! Deze formule ziet er in de grafiek uit als een parabool. Je wilt weten waar de parabool de X as snijdt –> X = ?
Je krijgt dus eerst een kwadratische vergelijking en vervolgens gebruik je de ABC formule om deze op te lossen!
(In de formule zie je een ± teken staan. Dit betekent dat je de formule twee keer doen. Eerst met + en dan met -. Later gaan we dit met een voorbeeld laten zien).
Om de formule te gebruiken, wil je eerst a b en c identificeren. Deze kan je dan in de formule invullen.
Opnieuw: ax² + bx + c = 0
a is de coëfficiënt van de term met x² (de kwadratische term),
b is de coëfficiënt van de term met x (de lineaire term),
c is de constante term (het getal zonder x).
Nu je deze hebt gevonden, ga je eerst de discriminant berekenen.
Wat betekent de discriminant?
Het stukje onder de wortel (b2-4ac) noem je de discriminant . Dit stukje van de formule laat zien hoeveel oplossingen de vergelijking heeft.
Dus, D staat voor “b2-4 ac “.
De discriminant (D) bij een kwadratische vergelijking geeft aan hoeveel oplossingen de vergelijking heeft en bepaalt hoe de bijbehorende parabool de x-as snijdt:
- Rood: D>0, heeft de vergelijking twee verschillende oplossingen. De parabool snijdt de x-as op twee punten.
- Zwart: D=0, is er één oplossing (dubbele wortel). De parabool raakt de x-as precies in één punt.
- Groen: D<0, zijn er geen reële oplossingen. De parabool snijdt de x-as niet.
Zo gebruik je de ABC-formule
Nu je weet hoe je de discriminant berekent kan je de ABC-formule toe gaan passen. Hieronder vindt je drie voorbeelden waarbij de discriminant verschilt zoals hierboven. Hiervoor gebruik je het volgende stappenplan
Voorbeelden van sommen met de ABC-formule
Hieronder vindt je drie voorbeelden waarbij de discriminant verschilt zoals hierboven. Het eerste voorbeeld rechts is helemaal uitgewerkt. Gebruik dezelfde methode om de andere twee voorbeelden na te rekenen.
- Voorbeeld 1: D>0
Stap 1: de formule is: x² – 5x + 6 = 0
Stap 2: a = 1, b = -5, c = 6
Stap 3: D = 1 –> twee oplossingen
Stap 4: Invullen geeft x = 2 en x = 3 - Voorbeeld 2: D=0
Stap 1: x² + 4x + 4 = 0
Stap 2: a = 1, b = 4, c = 4
Stap 3: D = 0
Stap 4: x = -2 - Voorbeeld 3: D<0
Stap 1: 2x² + x + 1 = 0
Stap 2: a = 2, b = 1, c = 1
Stap 3: D = – 7
Stap 4: Geen reeële oplossingen
Veelgemaakte fouten bij de ABC-formule
- Het gebruiken van verkeerde a, b of c (bijvoorbeeld verkeerde tekens)
- Het niet correct berekenen van de discriminant
- Plus/min vergeten bij ±
- Delen door alleen 2 in plaats van 2a
Tip!: controleer altijd stap voor stap
Oefenen met de ABC-formule
Wil je beter worden in het oplossen van kwadratische vergelijkingen met de ABC-formule? Op StudyGo vind je leuke en duidelijke oefenopgaven waarmee je kunt oefenen. Zo leer je hoe je de formule gebruikt en krijg je steeds meer vertrouwen in je eigen kunnen.
Veelgestelde vragen over ABC-formule
Lukt het nog niet helemaal met de ABC-formule? Geen zorgen! Met bijles wiskunde van StudyGo krijg je persoonlijke uitleg en kun je in je eigen tempo oefenen tot je het écht snapt.
Vraag wiskunde-bijles aan
